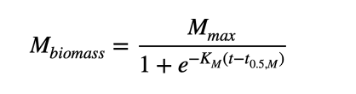In the intricate and dynamic ecosystems of forests, a crucial ecological process is unfolding that has significant implications for our planet’s carbon balance. Tropical forests are adept at producing 34% of oxygen [1]. This capability is not merely a passive feature of these ecosystems but a fundamental aspect of the photosynthetic process, wherein trees and plants convert CO2 and sunlight into energy, essential for their growth and sustenance.

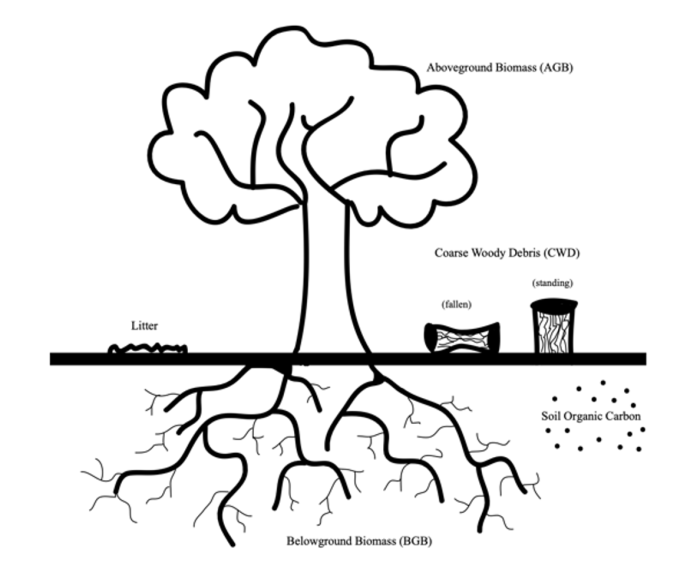
The role of CO2 uptake in forests extends far beyond mere carbon sequestration. It is intimately connected to trees’ growth and developmental dynamics, primarily through its influence on biomass accumulation. Biomass, in this context, refers to the sum of all organic material that constitutes a tree’s physical structure – a tangible indicator of its growth. Trees distribute this biomass in two primary compartments: Above-Ground Biomass (AGB) and Below-Ground Biomass (BGB) (Figure 1 [2]). Above-ground biomass encompasses the tree’s parts visible above the soil line, including the trunk, branches, leaves, and any fruits or flowers. Below-ground biomass consists of the roots, which, though less visible, are equally crucial for the tree’s stability and nutrient uptake.

Figure 1. Tree carbon pools

This distribution of biomass is central to understanding how trees store carbon. The CO2 absorbed from the atmosphere is assimilated into both AGB and BGB. As a tree matures, its capacity to sequester carbon increases, making older trees more efficient at absorbing CO₂. This relationship highlights the significance of forest conservation and the role mature trees play in mitigating climate change. By understanding and supporting these natural processes, we can enhance the capacity of forests to act as carbon sinks, thereby contributing to global efforts to balance our planet’s carbon cycle and combat the escalating challenges of climate change.

To accurately determine the amount of CO₂ absorbed by trees, two critical measurements are taken directly from the tree: its diameter, measured in cm, and its height, measured in meters. These measurements are essential for calculating both the Above-Ground Biomass (AGB) and Below-Ground Biomass (BGB). These biomass values are calculated based on a specific formula that incorporates these two parameters 9 [3].

AGB = 0.25 x D² x H

Where:

• AGB: Above-Ground Biomass (pounds).
• D: The tree diameter measured 1.37 meters from the ground (inches). This measurement is used globally as a standard to get better results. However, you can still use the formula if your tree is below 1.37 meters.
• H: The tree height (feet).

The overall green weight of the biomass is estimated to be 120% of the AGB value, based on the assumption that the BGB, which comprises the tree’s root system, accounts for approximately 20% of the AGB [3]. Therefore, BGB can be calculated as follows:

BGB = 0.2 × AGB

From these formulas, we can calculate the total biomass from a tree:

Total Biomass (TB) = AGB + BGB = AGB + 0.2 x AGB = 1.2 × AGB

On average, a tree consists of 72.5% dry matter and 27.5% moisture content. To calculate the tree’s dry weight, we could multiply the total weight of the tree by 72.5%.

Total Dry Weight (TDW) = TB × 0.725

Carbon occupies 50% of the total dry weight. Therefore,

Total Carbon (TC) = TDW × 0.5

With the value of total carbon, we can calculate the value of CO₂ equivalent sequestered on a tree. CO₂ has one molecule of Carbon and two molecules of Oxygen. The atomic weight of Carbon is 12u, and the atomic weight of Oxygen is 16u. The weight of CO₂ in trees is determined by the ratio of CO₂ to C is 44/12 = 3.67. Therefore, to determine the weight of carbon dioxide sequestered in the tree, multiply the weight of carbon in the tree by 3.67.

CO₂ weight = TC × 3.67

It is worth noting that the CO₂ weight above represents the CO₂ sequestered in the entire lifetime of the tree. To ascertain the annual or yearly rate of CO₂ sequestration, divide the total weight of CO₂ absorbed by the tree’s age.

What happens in the first ten years?

During the first decade of a tree’s life, trees experience rapid growth. High rates of CO2 absorption mark this period, as young trees require vast amounts of energy to fuel their development. This is important for the tree’s health and how well it grows. Therefore, a tree goes through complex development during the first ten years and needs energy.

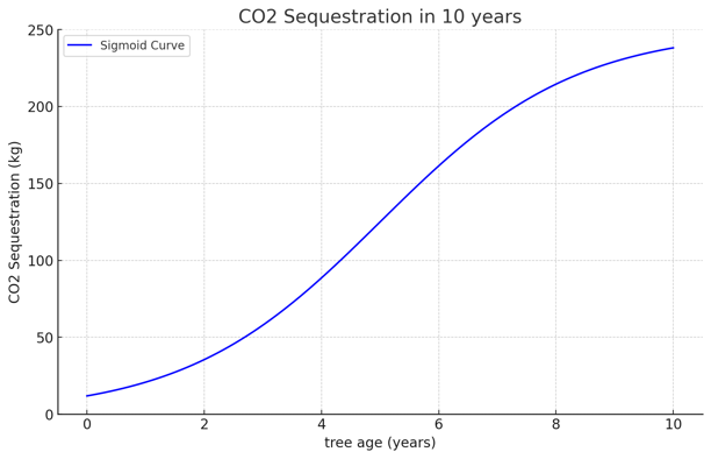
Figure 2. Sigmoid curve estimation for CO2 sequestration

The rate at which a tree absorbs carbon doesn’t follow a linear pattern; instead, it can be modeled by a sigmoid curve, which resembles an “S” shape. (Figure 2). The x-axis represents the tree’s age, and the y-axis shows how much carbon dioxide the tree absorbs in years. This graph could be generated from the following formula extracted from journal [4], where Km is the growth rate for a species, t represents the tree’s age, t_0.5,M represents the age where a tree can reach half of its maximum biomass, and Mmax is the maximum biomass a species can reach during its lifetime.

Figure 3. Formula

Conclusion 

Trees are vital in reducing the amount of carbon dioxide in our atmosphere. As they age, they become more efficient at sequestering carbon, which is essential to climate change mitigation. By understanding how trees store carbon, we can appreciate the significance of forest conservation and tree planting efforts.

Calculating the amount of CO2 sequestered by a tree not only helps measure environmental impact but also strengthens the case for reforestation and forest preservation. Every tree planted brings us one step closer to a more balanced carbon cycle and a healthier planet.

By preserving existing forests and promoting new tree-planting initiatives, we can harness nature’s power to combat the climate crisis. EcoMatcher is committed to leveraging technology to facilitate transparent and impactful reforestation efforts, offering everyone a chance to contribute to a more sustainable future.

Sources: 

[1] https://www.nationalgeographic.com/environment/article/why-amazon-doesnt-produce-20-percent-worlds-oxygen.

[2] DiRocco, T. L., Ramage, B. S., Evans, S. G., & Potts, M. D. (2014). Accountable accounting: carbon-based management on marginal lands. Forests, 5(4), 847-861.

[3] Shadman, S., Khalid, P. A., Hanafiah, M. M., Koyande, A. K., Islam, M. A., Bhuiyan, S. A., … & Show, P. L. (2022). The carbon sequestration potential of urban public parks of densely populated cities to improve environmental sustainability. Sustainable energy technologies and assessments, 52, 102064.

[4]  Paridar, Z., Ghasemi-Fasaei, R., Yasrebi, J., Ronaghi, A., & Moosavi, A. A. (2024). Applicability of the sigmoid model to estimate heavy metal uptake in maize and sorghum as affected by organic acids. Environmental Science and Pollution Research, 31(2), 3222-3238.